Penjelasan Mengenai Gerak Melingkar Beserta Pola Soal

Gerak Melingkar - Dalam materi ini kita akan mempelajari mengenai posisi sudut, kecepatan sudut, dan percepatan sudut sebagai persamaan fungsi terhadap waktu. Secara berturut-turut dinyatakan θ(t), ω(t), dan α(t).

1. Posisi Sudut

Posisi sudut dari suatu titik zat yang bergerak melingkar dinyatakan: θ =  θ(t), θ(t) merupakan fungsi dari waktu.

2. Kecepatan sudut

Grafik posisi sudut terhadap waktu

Kecepatan sudut rata-rata yakni hasil bagi perubahan posisi sudut dengan selang waktu tertentu, perhatikan gambar diatas!

(1)

Apabila selang waktu Δt mendekati nol, maka kecepatan benda tersebut yakni kecepatan sesaat, dirumuskan:

(2)

Kecepatan sudut sesaat merupakan turunan pertama dari fungsi posisi sudut terhadap waktu. Dalam sebuah grafik fungsi posisi sudut terhadap waktu (θ – t), kecepatan sudut sesaat ditentukan dari kemiringan grafik tersebut, perhatikan gambar berikut!

Kemiringan grafik mengatakan besarnya kecepatan sudut.

Jika β yakni sudut kemiringan garis singgung grafik – t, maka kecepatan sudut sesaat dituliskan:

ω = tan β

(3)

Posisi sudut sanggup dicari dari fungsi kecepatan sudut sesaat. Apabila kecepatan sudut suatu benda diketahui, kita sanggup memilih fungsi posisi benda dengan mengintegralkan fungsi kecepatan sudut tersebut.

dθ = ω .dt

Jika pada ketika t = 0 posisi sudut θ₀ dan pada ketika t = t posisi sudut θ , maka:

(4)

dengan:

θ₀ = posisi sudut awal (rad)

θ = posisi sudut ketika t (rad)

ω = kecepatan sudut (rad/s)

t = waktu (s)

3. Percepatan Sudut

Percepatan sudut rata-rata yakni perubahan kecepatan sudut tiap satuan waktu.

(5)

Jika selang waktu Δt mendekati nol, maka percepatan yang dimiliki benda yakni percepatan sesaat yang dirumuskan:

(6)

karena,

maka:

(7)

Percepatan sudut merupakan turunan pertama fungsi kecepatan sudut atau turunan kedua dari fungsi posisi sudut.

Dalam sebuah grafik kecepatan sudut terhadap waktu ( ω - t ), percepatan sudut ditentukan dari kemiringan grafik tersebut, perhatikan gambar berikut!

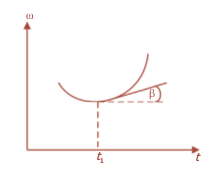
Kemiringan grafik mengatakan besarnya percepatan sudut.

Jika β yakni sudut kemiringan garis singgung grafik ω - t , maka percepatan sudut sesaat dituliskan:

α = tan β

(8)

Kecepatan sudut sanggup dicari dari fungsi percepatan sudut sesaat. Fungsi kecepatan sudutnya ditentukan dengan mengintegralkan fungsi percepatan sudut tersebut.

dω = α . dt

Jika pada ketika t = 0 kecepatan sudutnya ω₀ dan pada ketika t = t kecepatan sudutnya ω, maka:

(9)

dengan:

ω₀ = kecapatan sudut awal (rad/s)

ω_t = kecepatan sudut pada ketika t (rad/s)

α = percepatan sudut (rad/s²)

t = waktu (s)

Contoh Soal

1. Sebuah titik pada roda berotasi dengan persamaan posisi sudut θ = 2 + 2t² + t³, θ dalam radian dan t dalam sekon. Tentukan:

a. posisi sudut titik tersebut pada ketika t = 2 s,

b. kecepatan sudut rata-rata dari t = 0 hingga t = 3 s, dan

c. kecepatan sudut pada ketika t = 2 s!

Penyelesaian:

a. Posisi sudut

θ = 2 + 2t² + t³

t = 2 s → θ= 2 + (2)(2)² + 2³ = 18 rad

b. Kecepatan sudut rata-rata

t = 0 → θ₀ = 2 rad

t = 3 → θ₃ = 2 + (2)(3) + 3³ = 35 rad

c. Kecepatan sudut sesaat

t = 2 s → ω = (4)(2) + (3)(2)² = 20 rad/s

4. Kinematika Rotasi

a. Gerak Rotasi Beraturan

Gerak rotasi beraturan didefinisikan sebagai gerak rotasi dengan kecepatan sudut konstan atau percepatan sudut nol. Berdasarkan persamaan (4) diperoleh:

Karena kecepatan sudut Z konstan, maka:

(10)

dengan:

θ₀ = posisi sudut awal (rad)

θ_t = posisi sudut pada ketika t (rad)

ω = kecepatan sudut (rad/s)

t = waktu (s)

b. Gerak Rotasi Berubah Beraturan

Gerak rotasi berubah beraturan didefinisikan sebagai gerak rotasi dengan percepatan sudut konstan. Berdasarkan persamaan (9) diperoleh:

Karena percepatan sudut α konstan, maka:

(11)

Posisi sudut θ sanggup ditentukan dengan memasukkan persamaan (11) ke persamaan (4), sehingga:

(12)

dengan:

θ₀ = posisi sudut awal (rad)

θ_t = posisi sudut pada ketika t (rad)

ω₀ = kecepatan sudut (rad/s)

α = percepatan sudut (rad/s²)

t = waktu (s)

Contoh Soal

1. Sebuah benda dengan jari-jari 20 cm berotasi dengan percepatan sudut tetap 2 rad/s² . Pada ketika t = 0 s, kecepatan sudut dan posisi sudutnya masing- masing 5 rad/s dan 10 rad. Tentukan:

a. kecepatan sudut ketika t = 5 s,

b. kecepatan linier ketika t = 5 s,

c. posisi sudut ketika t = 3 s, dan

d. panjang lintasan yang ditempuh selama 4 s!

Penyelesaian:

Diketahui:

R = 20 cm = 0,2 m

ω₀= 5 rad/s

α = 2 ras/s²

θ₀ = 10 rad

Ditanya:

a. ω_t = ... ? (t = 5s)

b. v = ... ? (t = 5s)

c. θ_t= ... ? (t = 3s)

d . s = ... ? (t = 4s)

Jawab:

a.ω_0t = ω₀ + α . t = 5 + (2)(5) = 15 rad/s

b. v = ω .R = (15)(0,2) = 3 m/s

c. θ_t = θ₀ + ω₀ .t + 1/2 α . t² = 10 + (5)(5) + 1/2 (2)(5)² = 10 + 25 + 25 = 60 rad

d. s = T .R = (60)(0,2) = 12 m

2. Sebuah roda berputar dengan kecepatan 300 putaran per menit, lalu direm dan 5 sekon lalu kecepatannya menjadi 60 putaran per menit. Tentukan sudut roda tersebut!

Penyelesaian:

Diketahui:

ω₀ = 2π 300/60 = 10 π rad/s

ω_t = 2π 60/60 = 2π rad/s

t = 5 s

Ditanya:

α = ... ?

jawab:

ω_t = ω₀ + α . t

2π = 10 π + α (5)

5α = 2π -10 π

5α = -8 π

α = - 1,6 π rad/s²

Share this post